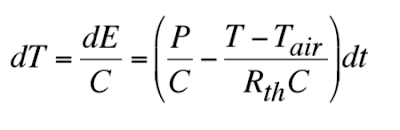Final Project Week 3

Day 21 (4/12/16)

During the third week of our final project, Sara and I made some major adjustments to our design. We decided to go a different way from our original idea of the temperature scale. Instead we decided to make a warning system for Jim. We planned to have 2 elements that would serve as a warning device for Jim. The first layer of warnings are LED lights. We planned to have a blue LED for when Jim starts to get cold and a red LED for when Jim gets too hot. For the second layer of warning systems we planned to have bell. Our idea was to use a servo to either ring the bell on a stick that is attached to it or to attach a stick to the servo to hit a bell.

Once we refined our idea for the device, we started putting our prototype together. While Sara worked on the code, I put together the circuit. Our first prototype ended up looking like this:

Day 22 (4/15/16)

We had a little bit of trouble with the code and the circuit doing what we wanted it to do but by playing around with the code and trying to simplify the circuit we were able to figure out our problems and fix it. By the end of the week we had all of the pieces (the LEDs and the servo) working properly. All were missing were the correct temperature ranges for Jim.

Here is the code we used for the circuit:

Here is a video of our working prototype:

The next steps for us is to attach the bell to the servo and then present our prototype to Jim to get feedback. Our meeting with Jim will be next week.

Thermal Systems using MATLAB Part 2

Day 19 (4/5/16)

Task #1:

The first part of the Thermal Systems #2 assignment asked us to generate an experimentally measured heating curve. To do this, we ran the test_thermal code:

and we ran it on our LogoChip, which looked like:

We got a resulting heating curve that looked like:

From this heating curve we can calculate the values of the thermal resistance (Rth) and the heat capacity (C). We calculated Rth by taking the total change in temperature (21.7 K) and dividing by the power (6.5 W). We determined that Rth was 3.34. We calculated C by dividing the power by the slope of the graph (0.2736). We determined that C was approximately 23.75. Using both the values of Rth and C, we multiplied them together to get the time constant tao which was 79.6. Tao is the time it takes for the system to reach about 63% of the asymptotic value. Our graph and our tao match to this definition because at a time of 79.6 seconds, the temperature reads about 321.8 K, which is about 60% of the final asymptotic value for the temperature.

To summarize the values:

Rth = 3.34

C = 23.75

Tao = 79.6

Task #2:

Our second task was to modify the heatsim code with our calculated quantities and see how similar our heat curve was to the simulation. Here was the plot from our simulation:

As you can see, both plots are pretty similar. Any differences that exist may be due to fluctuating ambient temperatures in the air or inaccuracies in our calculations. Also, the real world isn't perfect, so the perfect simulation will likely not match up exactly with the real heat curve.

Task #3:

Our third task was to use bang bang control to modify the test_thermal code to change the amount of power supplied to the system based on if the temperature is above or below the target temperature. In our case, the target temperature was 340 K and here is the modified code we used:

Here is the resulting plot from bang bang control for our thermal system compared with the simulation for bang bang:

Task #4:

Our final task was to use proportional control in attempts to reach our target temperature of 340 K. For a discussion on what proportional control is or how to set it up see my previous blog postings.

For our system, we tested the code with 3 different proportional gain coefficients (Kp). The values for Kp were given to us in the assignment with units of W/K, and since we were using percentages to determine how much power to deliver to the system we had to change the units. To do this, we divided the given Kp by the total power, 6.5 W, and multiplied by 100. This gave us resulting values of:

Kp1 = 0.77%

Kp2 = 2.08%

Kp3 = 7.70%

To plot the heat curve with proportional control using these values we used the following code:

And here is a resulting plot for proportional control using the smallest Kp:

The system does not reach the control set point when the gain is small because the constant only allows for a maximum of 30% power. Since the biggest the error could be is only about 40K and the constant is .77, the max power will be very low. Not having a lot of power will take the system a lot of time to reach the target temperature.

Here is the comparison of our simulation and the actual thermal system:

When the proportional gain is high, the temperature of the system shoots up at the beginning and levels off quicker, much like the simulation. The optimal gain setting for our thermal system seems to be a high gain because that gets us closer to the desired temperature because it shoots up higher at the start. Regardless of our chosen Kp though the temperature does not reach the target temperature. 

Final Project Week 2

Day 19 (4/5/16)

After discussing our ideas further, and after talking to Jim, Sara and I came up with our revised and improved idea for our final project. We decided that we are going to measure the temperature of Jim's extremities by attaching a temperature sensor to his ankles. The temperature sensor will be connected to the arduino that will allow us to alert Jim of his temperature and his temperature change. We decided that we are going to use a servo motor with a rod attached at the end that will move to show Jim his temperature. When he is getting too hot the servo will move toward the hot mark and when he is getting too cold, the servo will move in the other direction. This way, Jim will know when he needs to make a change and take care of his extremities temperature.

Day 20 (4/8/16)

Today we pitched our idea to Jim. He liked our idea, but also mentioned a project that MIT is working on that sounds very similar and more advanced than our project. MIT's project doesn't, however, seemed to be focused on Jim's extremities, so I think Sara and I will just continue forward with our plan.

Final Project Week 1

Day 16 (3/18/16)

Today the class split up in to two groups. One of the groups went to the child study center and the other stayed in the classroom and was visited by Jim Wice from disability services. Each of the groups learned about the problems that needed to be solved and were able to ask questions.

I was in the group that met with Jim Wice, and it was very interesting to hear what he had to say. He said that his main challenge was his body temperature. Often it fluctuates a lot and he won't notice that his body temperature is off until it has gotten very severe.

Meeting with Jim Wice, I knew that I wanted to work on a project that could help him and others with similar challenges.

Day 18 (4/1/16)

Sara, my final project partner, and I both came up with some initial ideas for the final project. Today we had to present these initial ideas in class

Sara's idea was to use a finger temperature sensor that would be connected to an arduino. When the temperature got outside of a certain range, the sensor would vibrate to let Jim know that his temperature was off.

My idea was to have a thermometer attached to Jim, probably the back of his neck, wherever it's best to take his temperature. The thermometer would be connected to the arduino that we could program with a certain desired temperature range. When Jim's temperature got too hot, a red led light would turn on and when Jim's temperature got to cold, a blue led would come on to let Jim know that he needed to make a change and get his body temperature back to normal.

Simulating Thermal Systems using MATLAB (Part 1)

Day 18 (4/1/16)

Our next project to develop our computer coding skills and understanding was using MATLAB to model the behavior of thermal systems. We worked with our final project partner, in my case Sara, to model the behavior of a cup of coffee using different techniques and using different parameters.

Question 1: How does the behavior of the cup of coffee change when we vary the thermal resistance (Rth) and/or the heat capacity (C).

Answer:
To answer this question we can simply look at the equation for the change in temperature:

As you can see, both Rth and C are in the denominator of the equation. So, when either of them is increased, the temperature will change (dT) by less. In other words, an increase in Rth or C will slow the drop in temperature of the cup of coffee.

We can also see this result by writing a script in matlab and varying both of those parameters to see what happens. Here is the script we used:

I using this script, I ran it multiple times changing just Rth, then just C and then changing both variables. Here is the plot I got of the different behavior for changing just Rth (the value of Rth for each line is listed in the text box at the top):

Here are the different behaviors for just changing C:

And here are the different plots for varying both Rth and C ( I plotted all possible combinations for increasing and decreasing Rth and C values):

As the plots show, increasing C and Rth will slow down the cooling process for a hot cup of coffee.

Question 2: Calculate a good value for P (power) if we want our coffee to heat up to 84 degrees C (356 K).

Answer:
This question gave us the revised equation for dT that included the introduction of a power source. Here is the revised equation:

And here is how I solved this equation for P with known values for C, T, Tair, and Rth:

A reasonable power amount is 74 watts.

Question 3: Simulate a temperature controller that uses bang bang control to reach and maintain the desired temperature. Why is bang bang control appropriate for many thermal systems? When might it be insufficient?

Answer:
To modify the code to include bang bang control, we used an if else statement so that when the temperature is above the desired 357K, there is no power delivered to heating the coffee and when it is below the desired temperature, we deliver 74W of power to the temperature controller. Here is what the code looked like:

And here is the plot for bang bang control:

Bang bang control is appropriate for many thermal systems because temperature takes time to vary. A change in the temperature of something is not very abrupt, so it is easy to maintain the temperature around the desired value. Also, with a lot of thermal systems, it is not crucial that the temperature be exactly the single temperature, so the small variance caused by bang bang does not cause any problems. Bang bang control will be insufficient when an exact temperature needs to be obtained and maintained. Bang bang will cause some minor fluctuations in temperature by turning on or turning off an external heat source, so for high accuracy thermal systems, you need higher accuracy than bang bang.

Question 4: Create a program that uses proportional control to reach and maintain the desired temperature. How does this approach compare to bang bang control?

Answer: 

To use proportional control you have to apply the concepts I talked about in my previous blog post (Sciborgs Part 3)

Strength = k * error

where k is the gain constant

and error = goal - reality

When this is applied to the code, it becomes:

Here is the resulting plot for proportional control:

The main difference between the effects of bang bang control versus proportional control is that at small times, proportional control has much larger changes in temperature than bang bang. But, after that initial rapid spike in temperature, proportional control levels off quickly and approaches the target temperature at a much slower rate. Interestingly, proportional control undershoots the target value and slowly works its way towards it, where as bang bang goes until it reaches the target temperature and then reacts.

Question 5: Modify your program to include a delay time for when the temperature sensor records the temperature. What is the impact of this sensor delay on your system in each case? What other delay(s) might you expect in your thermodynamic system, apart from sensor delays?

Answer:

For the bang bang control, to add in the delay, all you had to do was set the initial time equal to the delay. So the new code looked like this:

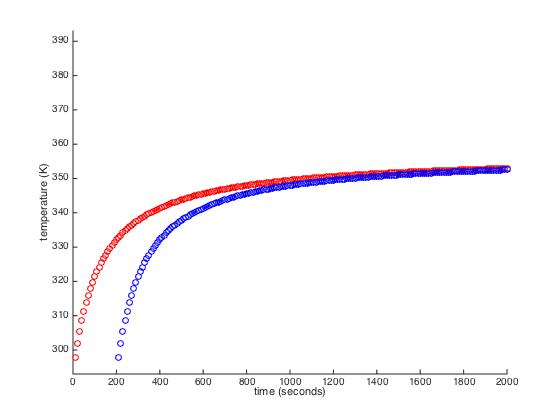
Compared to without the delay this is how the function behaved. The red is without the delay and the blue one is with delay:

Apart from the sensor delay, we can expect delays from the changing temperature. As I mentioned earlier, changing the temperature of something is not an abrupt task, it takes time to heat something up or cool it down. The delays from the sensor and the changing temperatures would likely continue to add up making the bang bang control system less and less effective.

For proportional control, I did the same thing to add the delay. I just added a variable called delay, which was whatever time value the delay was, and then set the initial time to the delay. I wont show the code becuase it is almost exactly the same with the exception of the two lines I changed (the exact same ones as bang bang). Here is how the delay effected the results (once again red is no delay, blue is delay) :

For the proportional delay system, there will also be the temperature delay that I mentioned for bang bang. However, all in all I believe the proportional system will be less effected by delay and will be more accurate in the long run.

MATLAB Introduction

Day 17 (3/29/16)

Today we started learning how to program in Matlab. By reading through chapters 1-4 of "Physical Modeling in MATLAB," by Allen B. Downey and going through some of the exercises, we were able to get a good understanding of MATLAB and some or its major functions.

The exercises are outlined below with screenshots of the code and the answers/graphs they produced if applicable.


Exercise 2.1: fibonacci1 script

The first exercise we did was come up with a script to determine the nth number in the fibonacci sequence.

Here is what the code looked like:

If you wanted to solve for the 10th value, you would input 10 when the command window prompts you for the value of n.

Exercise 2.3: car_update script

The second exercise we did was to create a script to update the number of cars in both Albany and Boston week to week. The conditions were that they both started with 150 cars and 5% of the cars from Albany go to Boston each week and 3% of the cars from Boston go to Albany each week.

Here is what the script looked like:

After running the script repeatedly, the number of cars finally reached an equilibrium after 24 weeks with 116 cars in Albany and 184 cars in Boston.

Exercise 3.1: car_loop script

The next task we did was update the car script to run it in a loop, rather than having to run the code for each week, we can specify the number of weeks we want to run the code for.

Here is what the new script looked like:

And here is what the loop returned after 52 weeks:

Exercise 3.2: car_loop script with plotting. Also try initial values of a & b = 10000

The next exercise we did was build on top of the car loop so that our data could be plotted to see the pattern. We did this by just adding a plot function in to the loop and specifying the shape and color of all of the points.

Here is what the script looked like:

Here is what the plot looked like for number of cars in Albany with an initial values of 150 at each location and a time span of 52 weeks:

And here is what the plot looked like for number of cars in Albany with an initial values of 1000 at each location and a time span of 52 weeks:

Exercise 3.5: fibonacci2 sequence script

The next exercise we did was to create a script using a loop to determine the nth element of the fibonacci sequence.

Here is what the code looked like:

For the 10th number in the sequence, the code returned a value of 144:

Exercise 4.6: plotting fibonacci ratios

The last exercise we had to do out of the book was to create a vector for both the fibonacci sequence and the fibonacci ratio (Fn+1/Fn). And then we had to plot the ratio.

Here is what my code looked like:

And here is what the plot of the fibonacci ratio vector looked like:

Unfortunately, I did not have time to get to the baseball problem, but I will take a look at it and try to work it out when I get the chance.